Level sets, the gradient, and gradient flow are methods of extracting specific features of a surface. You’ve heard of level sets and the gradient in vector calculus class – level sets show slices of a surface and the gradient shows a sort of 2D “slope” of a surface. These measurements are useful on their own, but they hint at something else, something more abstract. The gradient vectors are perpendicular to the level sets, so will always be direction the “slope” of a point toward another point on another level set. But how would you represent that? The answer is the concept of gradient flow. Read more to learn about how these three standard measurements fit together to flow along a surface, much like a liquid or rolling object.
Continue reading “Level Sets, the Gradient, and Gradient Flow”
Tag: math
Visualizing multivariable functions and their derivative
In a first course in calculus, many students encounter an image similar to the following:
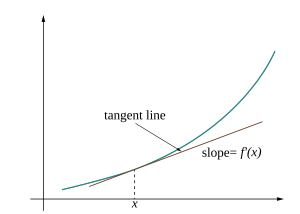
Such an illustration highlights a key property of the single variable derivative: it’s the best linear approximation of a function at a point. For functions of more than one variable, the derivative exhibits this same characteristic, yet there is no obvious corresponding picture. What would an analogous visualization look like for a multivariable function?
For the past few weeks, I’ve been working towards a visualization of multivariable functions and their derivatives. Check out the end result here, or read on to hear about my process. I assume some knowledge of calculus and mathematical notation.
Continue reading “Visualizing multivariable functions and their derivative”
