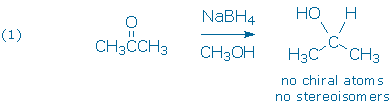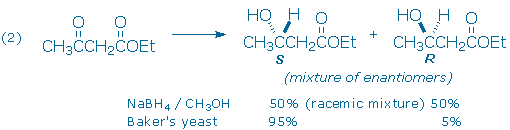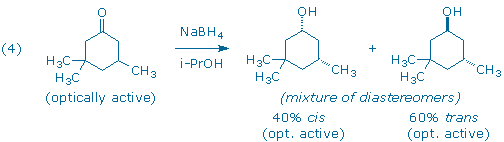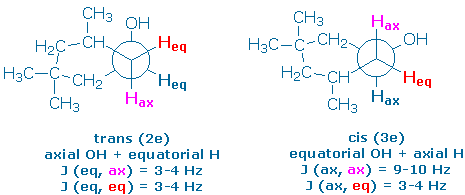Synthesis and Purification of Diastereomers: Sodium Borohydride Reduction of a Chiral Ketone
Background
A single compound can exhibit many types of isomerism. Even when the compound’s structure is relatively simple, chemical transformations may lead to unexpected mixtures of isomers. The following sections discuss possible stereochemical outcomes for ketone reduction, and spectroscopic methods for distinguishing stereoisomers.
General stereochemical principles
As you will see, the reduction of a ketone carbonyl can result in a number of stereochemical scenarios depending on the exact structure of the starting ketone.
The first and most straightforward example (1) is the reduction of a symmetric ketone, such as acetone. This reaction gives a single achiral product.
A second example (2) illustrates the selective reduction of a ketone carbonyl group and the creation of a new chiral atom. The newly formed chiral center is the only chiral center in the product and two outcomes, S and R enantiomers, are possible. In this case, the carbonyl carbon in the reactant is said to be prochiral, indicating that it can become a chiral center after a specific reaction, in this case, reduction.
The conversion of an achiral starting material into an optically active product is possible, but only if optically active reagents are used. Sodium borohydride is an achiral reagent, and optically inactive, so it necessarily reduces ethyl acetoacetate to a 50:50 racemic mixture of chiral alcohols. However, when the reduction is carried out with Baker’s yeast, the S-alcohol is produced in 90% optical yield instead (note: optical yield = %major enantiomer – %minor enantiomer). Baker’s yeast is able to achieve this outcome because it contains chiral enzymes called dehydrogenases. Like sodium borohydride, dehydrogenases are capable of catalyzing the selective reduction of the ketone carbonyl group in ethyl acetoacetate. The ester carbonyl group is not altered. Because yeast contains only one enantiomer of each type of dehydrogenase enzyme, these enzymes can be labeled as optically active reagents.
Before we leave example (2), you might wonder how chemists are able to distinguish the outcomes of these experiments. Recall that enantiomers possess identical chemical and physical properties. For example, the NMR spectra of the pure S and pure R alcohols are identical. And so are the NMR spectra of the 50:50 and 95:5 product mixtures! The traditional method for identifying enantiomers and mixtures of enantiomers is to measure their optical rotation of plane-polarized light. Enantiomers rotate light by the same amount, but in opposite directions. The racemic 50:50 mixture obtained from the NaBH4 reduction does not rotate plane-polarized light and is optically inactive. The 95:5 S:R mixture obtained from yeast is optically active: [a]D = +38.6o.
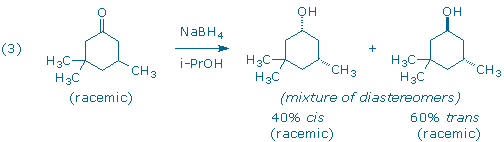
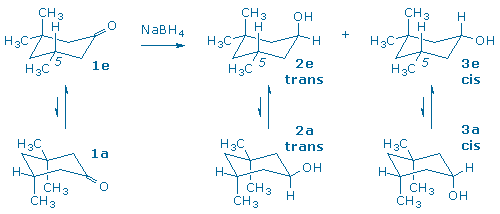
A third carbonyl reduction scenario, and the one you will explore in this experiment, involves the reduction of a molecule that contains a prochiral ketone and an additional chiral center (3). The products of the reduction all contain two chiral centers, so one must keep track of both enantiomeric and diastereomeric relationships between product molecules.
The diastereomers in (3) are distinguished by the labels cis and trans that indicate the relative positions of the hydroxyl and “lone” methyl groups. The diastereomers possess different relative configurations (they are neither superimposable nor mirror-images), and also different chemical and physical properties which makes them relatively easy to detect and identify in our laboratory.
Although the starting ketone in (3) is a chiral molecule, you will use a racemic mixture of the ketone in your experiment. As a result, your experiment will generate racemic mixtures of the cis and trans products. (Note: it is the habit of organic chemists to draw only one of the two possible enantiomers when depicting racemic compounds. In this particular case, each product has been drawn with the lone methyl group “down” even though the products with the methyl group “up” are present in equal amounts.) If we had provided you with an optically active sample of 3,3,5-trimethyl-cyclohexanone, as shown in (4), you would have still obtained the same 60:40 ratio of trans and cis diastereomers as in (3), but each diastereomer would now be optically active. (Can you see why?)
Properties of trans and cis 3,3,5-trimethylcyclohexanol
In this experiment, 3,3,5-trimethylcyclohexanone (1), a racemic ketone with one chiral center, is reduced with sodium borohydride to produce two alcohols, trans 2 and cis 3.
In order to understand the relative chemical and physical properties of these two diastereomers it is useful to know the conformational preferences of these molecules. One analysis is shown in the following figure (you might want to refresh your knowledge of the conformational analysis of cyclohexanes: see Sorrell, section 3.3).
Two chair conformations are possible for the starting ketone, and two conformations are also possible for each product. One way to differentiate between these conformers is to watch the 5-methyl group. Conformers 1e, 2e, and 3e, contain an equatorial 5-methyl group, while conformers 1a, 2a, and 3a, contain an axial 5-methyl group.
We assume that the 5-methyl group always prefers to be in an equatorial position (in other words, ‘e‘ conformers are preferred). The energy difference between an equatorial and axial methyl group is 1.8 kcal/mol. This energy is known as the methyl group’s A-value and is often used as an indication of steric bulk.
The hydroxy group also prefers to be in an equatorial position, however, its A-value is only 0.7 kcal/mol. (This makes sense since a hydroxy group has less steric bulk than a methyl group.)
Since two groups change places when the conformers interconvert, we might try to predict the lower energy conformer by adding A-values together. This suggests that cis 3e is more stable than 3a by 2.5 kcal/mol (= 1.8 + 0.7). It also suggests that trans 2e is more stable than 2a by 1.1 kcal/mol (= 1.8 – 0.7) even though 2e places the hydroxy in an axial orientation.
To summarize, this conformational analysis of the two diastereomeric alcohols suggests that the trans alcohol, 2, will tend to keep the OH axial, while the cis isomer, 3, will have an equatorial OH.
It is well documented that functional groups in an axial orientation are sterically more hindered than their equatorial counterparts. The enhanced accessibility of an equatorial hydroxy group can be seen from the following facts:
- the boiling point of the cis isomer is higher than the trans isomer (see Procedure)
- the cis isomer runs slower on silica gel than the trans isomer (you will document this for yourself during this experiment)
- the cis isomer reacts five times faster than the trans isomer with acetic anhydride in pyridine
While one could attempt to assign the cis and trans diastereomers based on the types of observations summarized above, more compelling structural proof is needed. Chemists have come to rely heavily on spectroscopy as a method of structural identification. This is especially true for more subtle structural features, such as the relative stereochemistry of two chiral atoms.
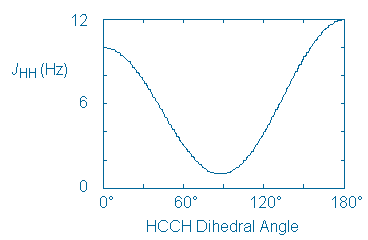
Since the cis and trans compounds are diastereomeric, they produce different IR and 1H NMR spectra. Unfortunately, these differences are only useful to us if there is a way to to tell which compound has produced each spectrum. Therefore, we need to identify a spectroscopic feature that will act as a stereochemical signature of each alcohol. One such signature is the value of the coupling constant (J) between adjacent or vicinal protons.
The following curve shows the relationship that typically exists between J and the dihedral angle between vicinal protons.
This curve can be applied to chair cyclohexane rings in a straightforward way. Vicinal axial protons create an HCCH dihedral angle of 180o and, according to the curve, will couple strongly. On the other hand, axial-equatorial and equatorial-equatorial proton pairs create smaller HCCH angles (60o) and will couple only weakly.
The following Newman projections show the preferred conformer of each alcohol, along with the orientations of the hydroxy groups and some nearly protons (you might want to make a model of your own so that you can see these relationships more clearly). The projections also show you the dihedral angles between the “alpha proton” (the proton next to the hydroxy group) and its neighboring vicinal protons.
The alpha proton in the trans alcohol (2e) is equatorial. It makes 60o dihedral angles with the four vicinal protons and should couple weakly to all of them. Therefore, we expect a pentet pattern (J = 3-4 Hz) for the alpha proton in 2e.
The alpha proton in the cis alcohol (3e) is axial. It should couple strongly to the vicinal axial protons and weakly to the vicinal equatorial protons,. We expect to see a triplet of triplets (J = 9-10, 3-4 Hz).
If these predictions are borne out, the coupling patterns produced by the alpha protons will serve as stereochemical signatures for the trans and cis alcohols. We shall see!
Molecular modeling
Organic chemists frequently rely on the types of arguments found in the preceding sections. Despite this, many of our arguments rely on questionable assumptions and these assumptions deserve closer scrutiny.
For example, in guessing the preferred geometry of each alcohol, we assumed that the three methyl substituents and hydroxy substituent do not distort the molecule’s geometry, that is, we assumed each ring adopts the same shape as chair cyclohexane. We also assumed that each substituent acts independently on conformer stability. And we assumed that interactions between substituents are not important.
These assumptions are convenient, but a convenient assumption is not necessarily a reliable one. Therefore, as part of this experiment, you will use molecular modeling to calculate the geometry of each alcohol and see if you obtain the same conformational predictions and HCCH dihedral angles given above.
Specifically, you will use Spartan’20 to build a model of every alcohol conformer that you can think of, and then calculate its equilibrium geometry and strain energy (“strain energy” is the appropriate term because you will be using molecular mechanics calculations). The lowest energy conformer of each alcohol represents that alcohol’s preferred geometry, but an alcohol might still exist as a mixture of conformers, so you will look at the relative energies of different conformers to work out the alcohol’s conformational equilibrium. In addition, you will be able to use the HCCH dihedral angles in this structure to interpret your NMR spectra. Your models will also tell you whether the simplifying assumptions made above were justified or not.