Distillation of a Liquid Mixture

This experiment consists of two distinct parts. In the first part, you and a partner will work together to distill an “unknown” (mystery) mixture of two liquids (chemists call this a binary mixture) using two different experimental techniques: simple distillation and fractional distillation. In the second part, you and your partner will investigate the distillates you collected in the first part using infrared (IR) spectroscopy. You will make experimental measurements and you will also look at predictions based on molecular models.

This is an easy experiment to conduct, but it may appear complicated because you are being asked to perform several different experiments, collect several kinds of data, and learn many new concepts. It may help you to consider the learning goals that we have for this experiment as you proceed.

The learning goals for distillation include learning to: 1) assemble and use two distillation apparatuses, 2) make temperature and volume measurements on distilling liquids, 3) use temperature and volume measurements to guide a distillation, i.e., use these data to make decisions about when to switch receiver vessels, and 4) appreciate the limitations of different distillation techniques. The information you need to learn about distillation is presented in the following sections on this page.

The learning goals for IR spectroscopy are quite different. They include learning to: 1) understand the physical phenomena that underlie IR spectroscopy, 2) connect IR absorptions with molecular structure (using molecular models and characteristic frequency tables), 3) prepare a neat liquid IR sample, and 4) make and notate IR measurements. The identification of unknown compounds using IR spectroscopy is an important skill that all organic chemists need to master, but most of the information covering IR is not presented in the lab manual. Look for presentations on IR spectroscopy to be made in class and for suggestions about IR-related material to read in your textbook.

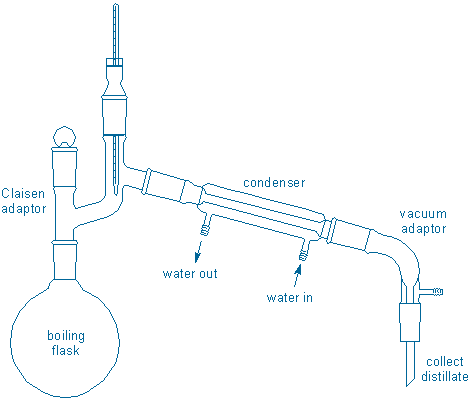
Distillation involves boiling liquid in a special apparatus called a distillation apparatus or, more colloquially, a “still.” A simple still is shown below:

The action in this still starts on the lower left in the boiling flask. This flask holds the liquid to be distilled. Heat is applied to the boiling flask (heater is not shown) causing the liquid to boil. Gas molecules travel upward out of the flask, then move up and to the right through some tubing (the Claisen adapter), before eventually reaching a water-cooled condenser. The gas cools inside the condenser and changes back into a liquid. Finally, the liquid (or distillate) continues moving to the right before dripping down through some more tubing (the vacuum adapter in this example) into a receiver of some sort (receiver is not shown, but it could be a test tube, a graduated cylinder, a collection flask, or “cow“).

Take a moment to trace the path of the molecules through the apparatus shown in the figure. Identify the places where liquids will be and the places were gases will be. Also identify places you expect to be hot to the touch (because they contain hot liquids or gases) or cold to the touch (because they contain cold liquids or gases).

You may have also noticed that the still contains a thermometer. The thermometer bulb is located near the terminus of the “hot gas” zone. Once hot molecules pass over the bulb they will enter the condenser and get cooled. This means the thermometer provides information about the nature of the gas that is about to be condensed. The thermometer does not provide any information that is directly related to the liquid in the boiling flask.

If we strip distillation down to its most basic functions, we see that it accomplishes only two things: it converts a liquid into a gas, and then it converts the gas back into a liquid. This might seem like a pointless closed loop, but distillation is useful for several reasons. First, it can be used to measure a liquid’s boiling point (bp). If the gas reaching the thermometer is pure (a single compound), its temperature will equal the boiling temperature of the liquid form of this gas. Second, distillation can be used to separate volatile materials from nonvolatile contaminants, such as hair or dirt. The contaminants remain in the boiling flask while the volatiles collect in the receiver. The third and most common reason for performing a distillation, however, is to separate the components of a liquid mixture. Imagine you had been given a 50:50 mixture of benzene (PhH, bp 80^oC) and toluene (PhCH₃, bp 111^oC) and you were asked to separate the compounds in the mixture. Benzene’s lower boiling point means that it is more volatile than toluene. Therefore, when this mixture comes to a boil, more benzene molecules will enter the gas phase and the liquid that collects in the receiver will be mostly benzene (at least initially). If we perform this procedure correctly, we can obtain a distillate that is mostly benzene and a residue (the liquid in the boiling flask) that is mostly toluene.

Unfortunately, distillations can be finicky. One distillation might produce relatively pure liquids and another might not. Some of this variability can be blamed on the distillation procedure itself, but some is due to choices made by the person performing the distillation. The following sections describe some of the theoretical principles that underlie distillation. These will help you understand when distillations will work (provide pure distillates) and when they won’t. They will also help you understand how the choices you make will determine the results from any distillation.

Distillation is set in motion by boiling a liquid. In our case, this liquid will be a mixture, but before we look into that, let’s review what happens when a pure liquid boils. We will begin by constructing a ‘molecular’ picture of the boiling liquid, and then connect this picture to macroscopic phenomena like evaporation, boiling, temperature, and pressure.

The most important thing to realize about any substance is that the molecules in that substance are always in motion. This means that a liquid that looks perfectly uniform and unchanging is really (if we could look closely enough) a surging mass of agitated molecules, all moving at random speeds in random directions, and all constantly colliding with neighboring molecules. Furthermore, each molecule’s behavior is constantly changing. Every collision transfers some energy from one molecule to another and changes the directions and speeds of the molecules. If you would like a human analogy, you could try imagining the molecules as people on a very crowded dance floor with an up-tempo band and all of the dancers wearing thick blindfolds.

The picture that we’ve just described is incredibly complex. A typical drop of liquid water contains about 10²⁰ molecules so a complete catalog of what is going in a water drop at any moment would have to list the positions, speeds, and directions of 100,000,000,000,000,000,000 molecules. Obviously, such a catalog cannot be constructed, but this doesn’t mean we cannot say anything about the molecules and their behaviors.

Students who take Chemistry 332 will learn that chemists can calculate the average speed of the molecules in a liquid, and also the speed distribution, i.e., the curve that shows how probable it is that any molecule might be moving half (or twice, or ten times) the speed of the average molecule. These calculations are beyond the scope of this course, but we can make use of the following facts: most molecules in a typical liquid move at speeds near the average speed (exceptionally slow/fast-moving molecules are rare), and the average speed tracks with a liquid’s temperature (raising the temperature raises the average molecule’s speed).

So far we have been thinking about a liquid as something that extends far in every direction, but if we consider the molecules that are right at the liquid’s surface, we can see that collisions might cause some special behavior. If a collision gives a surface molecule a strong enough “kick,” the molecule might be ejected from the liquid and enter the gas phase. High energy collisions like these are probably rare under most conditions so the rate at which molecules spontaneously leave a liquid will be fairly low. On the other hand, if we heat the liquid, we will make this kind of collision more frequent.

High energy collisions also occur deep inside a liquid. Here a “kicked” molecule will move just a short distance before it dissipates its energy by “kicking” other molecules. If the temperature is high enough, however, high energy collisions will become so frequent that groups of high energy molecules will form in the same vicinity. When a group of high energy molecules forms, they establish a zone of high energy, fast moving molecules inside the liquid. If this zone is large enough, it will appear to us as a gas bubble.

So far we have been focusing on ‘molecular’ pictures, but each of these pictures corresponds to something we can observe for ourselves, i.e., to some sort of macroscopic phenomenon. When we raise the average speed of the molecules in a liquid, the liquid feels hot to the touch. A thermometer inside this liquid would register a higher temperature. When fast moving molecules near the surface are ejected into the gas phase, a smaller amount of liquid remains. This behavior is what accompanies evaporation. Finally, when gas bubbles form inside a liquid, we say the liquid is boiling.

We can also quantify these macroscopic behaviors. If we place a liquid in a closed container and hold the temperature, T, constant, the molecules in the liquid and gas phases will come into equilibrium because the number of molecules being ejected from the liquid will eventually be matched by the number of molecules returning to the liquid. The partial pressure created by the gas molecules is called the liquid’s vapor pressure or P_v. Generally speaking, vapor pressure rises with temperature because gas phase molecules can store more energy per molecule than liquid phase molecules.

The rate of evaporation rises with vapor pressure, but something special happens when the temperature is high enough to make P_v equal to the external air pressure, P_ext. At this point vaporization can occur inside the liquid and not just at the surface. In other words, bubbles form in the liquid and the liquid boils. Once boiling has been initiated, adding more energy to the system will simply convert the liquid into gas bubbles at a faster rate, but the temperature will not rise. Let’s repeat that: a liquid’s temperature cannot be raised above its boiling temperature, i.e., above the temperature where P_v = P_ext.

A tangent: The fact that liquids cannot be heated to temperatures above their boiling temperatures makes for an interesting lesson for student cooks. Consider two college students trying to boil an egg for breakfast. The first student attends Reed College in Portland, Oregon (elevation 0 ft). At this elevation P_ext is typically 760 mm Hg (1 atm). Because water boils at the temperature where P_v = P_ext = 760 mm Hg, the Reedie can boil the egg at 100^oC. Eggs cook quickly at this temperature and the Reedie is able to finish her breakfast in just a few minutes. The second student, however, attends Colorado College in Colorado Springs, Colorado (elevation 6000 ft). At this altitude the air pressure, P_ext, typically hovers around 610 mm Hg. This student’s water will boil at only 94^oC. It’s pointless to add more heat because we know that this will just make the water boil more vigorously, it won’t raise the water temperature. So cooking occurs at a lower temperature, it takes longer for the egg to cook, and this student will probably be late to class. =(

This experiment involves distilling a mixture of two liquids, A and B, in order to separate and identify them. Based on what you know about pure liquids, you might imagine that this distillation will follow a sequence of steps:

1. boiling begins when the temperature in the boiling flask matches the boiling point of the lower boiling liquid (call this A)
2. molecules of A leave the boiling mixture and collect in the receiver; because the molecules pass over the thermometer bulb, the measured temperature, T, registers the boiling point of A
3. after A is exhausted from the mixture, boiling resumes when the temperature in the boiling flask rises to match the boiling point of the higher boiling liquid (B)
4. molecules of B leave the boiling flask, collect in the receiver, and T equals the boiling point of B.

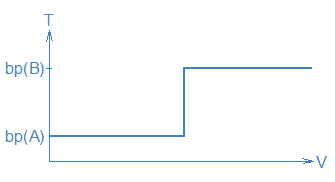
If one plotted the volume of liquid, V, collecting in the receiver (horizontal axis) against T (vertical axis), one would expect to obtain a graph that looks like this:

The long horizontal parts of the curve represent periods where the measured temperature, T, stays constant, i.e., a period during steps 1/2 when T = bp(A) and another period during steps 3/4 when T = bp(B). Because different temperatures correspond to different compounds collecting in the receiver (i.e., step 2 versus step 4), you can use T as an indicator of what compound is being collected.

The temperature measurements also tell you how to separate A from B. When T starts to rise between steps 1/2 and steps 3/4 you should replace the receiver containing A with a clean receiver in order to collect B. The separate portions of distillate are commonly called fractions so another way to state this is: collect two fractions, a low T fraction (A) and a high T fraction (B).

Unfortunately, most mixtures don’t follow this simple-minded picture, but the picture is still useful. First, the picture shows how we want a distillation to work (and how it needs to work if we are going to achieve complete separation of A and B). Second, it shows us how temperature and volume data can be used to guide a distillation procedure, namely, we collect fractions at particular temperatures and we switch receivers when the distillate temperature changes.

The reason that this picture is misleading is quite elementary: it assumes that the liquids vaporize independently so that vapor produced by the boiling liquid is pure A. In fact, molecules of A and B are both present in the gas phase so the vapor is a mixture. Because the vapor is a mixture, its vapor pressure,  P_v(mix), depends on the vapor pressures of both A and B (not just A as in our simple picture). As a rule, P_v(A) > P_v(mix) > P_v(B) so the mixture will boil at a temperature somewhere between bp(A) and bp(B).

Note: the previous statement, which can be restated as bp(A) < bp(mix) < bp(B), holds only for homogeneous mixtures, i.e., mixtures of fully miscible liquids. Heterogeneous mixtures made up of immiscible liquids are not uniform in all parts of the mixture and they exhibit different behavior. The distillation of heterogeneous mixtures will be discussed later in the semester.

It is helpful to explore these ideas in a few different ways. The next section provides a mathematical treatment of mixtures, which is followed by a section that uses data from an actual mixture.

Before introducing equations for vapor pressure, let’s adjust our terminology. The amount of gas produced by a single compound is given by the compound’s vapor pressure or P_v. When we have a gaseous mixture, the contribution of each compound to the total gas pressure is called the compound’s partial pressure or P_p. We have said that the gas in the boiling flask is a mix of A and B so, assuming everything behaves as an ideal gas, the vapor pressure of the mixture, P_v(mix), is just the sum of the partial pressures of A and B:

P_v(mix) = P_p(A) + P_p(B)

When a liquid mixture is homogeneous and ideal, we can also invoke another rule and say that the partial pressure of each compound is the product of its vapor pressure, P_v, and mole fraction, X:

P_p(A) = X(A) P_v(A)

P_p(B) = X(B) P_v(B)

Combining these equations gives the following:

P_v(mix) = X(A) P_v(A) + X(B) P_v(B)

This is beginning to look a little complicated so let’s back up for a moment. First, what do we mean by mole fraction? X(A), the mole fraction of A, is the fraction of all molecules in the mixture that are A. Mathematically, X(A) is obtained by dividing the number of molecules of A, N(A), by the total number of molecules in the mixture, N(A) + N(B).

X(A) = N(A) / {N(A) + N(B)}

X(B) = N(B) / {N(A) + N(B)}

Because A and B account for all of the molecules in the liquid, the two mole fractions must add up to one, i.e., X(A) + X(B) = 1. (Note: we could have called X the molecule fraction, but tradition dictates that we call it the mole fraction.)

Fractions X(A) and X(B) can also be seen as weighting factors. If a mixture contains 1 mole of A and 1 mole of B, there are 2 moles of liquid total and the mixture is weighted equally between A and B, i.e., X(A) = X(B) = 0.5. On the other hand, if a mixture contains 1 mole of A and 9 moles of B, the mixture is heavily weighted towards B, and X(A) = 0.1 and X(B) = 0.9.

Now let’s return to the equation for the vapor pressure of the mixture, P_v(mix). It is just a weighted average of the vapor pressures of A and B.

P_v(mix) = X(A) P_v(A) + X(B) P_v(B)

If we have a 50:50 mixture, the mixture’s vapor pressure will be a 50:50 average of the two vapor pressures, P_v(A) and P_v(B). On the other hand, if we have a mixture that is weighted more towards B, the mixture’s vapor pressure will be much closer to P_v(B).

Regardless of a mixture’s composition, the following will always be true, P_v(B) < P_v(mix) < P_v(A). To put it another way, adding B to A depresses the vapor pressure of the mixture (makes it more like B) while adding A to B increases the vapor pressure.

Mixtures obey the same fundamental boiling rule as pure liquids: a mixture boils when P_v(mix) = P_ext. Based on what we now know about P_v(mix) you should be able to see where our first picture went astray. Instead of boiling occurring at T = bp(A), we would have to heat the mixture to a somewhat higher temperature, T > bp(A). This is because the presence of B in the mixture makes P_v(mix) < P_v(A).

We can also spot another error in our initial picture. We had previously assumed that only molecules of A entered the gas phase, but now we see that both A and B molecules enter the gas phase. Because we want to separate A from B we should examine the number of A and B molecules that are present in the gas. If we assume that A and B both behave as ideal gases, their relative numbers are given by:

N_gas(A)/N_gas(B) = P_p(A)/P_p(B) = {X(A) P_v(A)}/{X(B) P_v(B)}

N_gas(A)/N_gas(B) = {X(A)/X(B)} {P_v(A)/P_v(B)}

The right-hand side of the lower equation rearranges mole fractions and vapor pressures in a useful way. X(A)/X(B) is the relative number of A and B molecules in the liquid. P_v(A)/P_v(B), on the other hand, reflects the relative volatility of A and B. Because we have assumed that P_v(A) > P_v(B), we know that P_v(A)/P_v(B) > 1. Introducing this inequality back into the lower equation gives a new inequality:

N_gas(A)/N_gas(B) > X(A)/X(B)

This inequality tells us that the A:B ratio is greater in the gas than the liquid. In other words, a vapor is enriched (relative to the liquid) in the more volatile compound. So while our simple picture was wrong – it is not possible to create a vapor that contains only A – the situation might still be promising because the vapor will be enriched in A. This A-enriched vapor enters the condenser, turns back into a liquid, and collects in the receiver, so the liquid we collect is enriched in A as well. Distillation can achieve enrichment. This is what makes distillation useful, if imperfect.

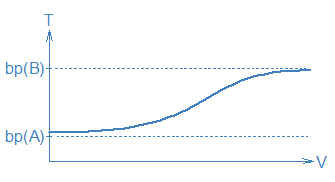
Actually, distillation is not only imperfect, it is also difficult. In our original picture, we had assumed that there would be long periods when things did not change, e.g., the long stretches on the T vs. V graph when T was constant and only one compound was collected in the receiver. This is entirely wrong. In a real distillation T will be rising (but not necessarily in a linear fashion) and the composition of the liquid in the receiver will be changing too. To see why, imagine that we begin boiling a 50:50 A:B mixture. The gas is enriched in A so A will be removed from the liquid mixture faster than B. Before too long, we will have a 49:51 A:B liquid mixture with a slightly lower vapor pressure and a slightly higher boiling temperature. This new liquid mixture will produce a new mix of A and B molecules in the gas phase. The temperature of this new gas mixture will be a little higher and its composition will be a little different from what came before. So, instead of constant temperatures and compositions, everything will be changing all the time. A real V vs. T graph would probably look more like the heavy line in the following graph:

One way to make these predictions more meaningful is to examine actual data. The following table contains information about some mixtures of cyclohexane (Cy) and toluene (Tol). See how much of these data you can understand given what you have just read.

liquid composition (mole Tol : mole Cy)	gas composition (mole Tol : mole Cy)	liquid boiling temperature (oC)	gas condensation temperature (oC)
0:100	0:100	81	81
20:80	4:96	84	82
40:60	12:88	88	83
60:40	26:74	94	86
80:20	48:52	102	91
100:0	100:0	110	110

The left side of the table contains composition data. The left-hand column describes different mixtures that might be placed in a boiling flask (notice that the top and bottom entries are not actually mixtures, they refer to pure cyclohexane and toluene, respectively.) and the adjacent column describes the gas mixtures produced by the boiling liquids. Notice that every liquid mixture produces a gas mixture. Also, the gas is always enriched in the more volatile component, cyclohexane (Cy). The 20:80 and 40:60 liquids produce gases that contain roughly 90% cyclohexane or better. Even the 60:40 and 80:20 liquids produce gases that contain somewhat more cyclohexane than toluene.

The right side of the table contains temperature data.  The third column reports the boiling temperature of the liquid. Normally this temperature is not be measured so we should examine these numbers carefully. Notice that bp(mix) rises as the proportion of toluene rises and that bp(Cy) < bp(mix) < bp(Tol) for all mixtures.

The last column reports T, the temperature registered by gas condensing on the thermometer bulb. For mixtures, the gas temperature is always lower than the liquid temperature. This follows from the fact that the gas mixture is enriched in cyclohexane. Even so, T(mix) > bp(Cy) for every mixture.

As a final exercise, let’s imagine how a distillation of a 50:50 Tol:Cy mixture might proceed (and also try to think about how this description differs from the simple picture we laid out above).

1. To get the mixture to boil, we will need to heat the liquid to about 91^oC. This is well above bp(Cy), 81^oC.
2. The gas produced will contain at least 80% Cy, a substantial enrichment over the 50% Cy in the original liquid. The temperature reported on the thermometer bulb, T, will be only about 85^oC, which might encourage us to think that the distillate is pure. It is not.
3. As the distillation continues, the liquid will become depleted in cyclohexane and we will need to supply more heat to keep it boiling. However, because we are only monitoring the gas temperature, T, we will detect only a slow, modest rise in the reported temperature from about 85^oC to 91^oC. At this point the cyclohexane portion in the liquid will have fallen to 20%. Continuing the distillation will cause the cyclohexane portion to drop rapidly.
4. As the cyclohexane fraction falls further, the gas temperature, T, rises rapidly from 91^oC to over 100^oC. The gas finally contains more toluene than cyclohexane.
5. Finally, as the liquid becomes almost entirely toluene, the distillation begins to operate like the distillation of a pure liquid and the measured temperature, T, approaches bp(Tol), 110^oC.

This description should persuade you that distillation can achieve something (enrichment) if not exactly what you want (perfect separation). In principle, you could maybe collect a cyclohexane-rich fraction during the time that T is rising slowly and still well below 90^oC. You could likewise collect a toluene-rich fraction when T is rising slowly and well above 100^oC. The material that collects between these temperatures (when T is rising more rapidly) is not substantially enriched in either compound. It could be discarded or it could be saved for additional processing.

Given these complexities, the trick to a “successful” distillation is to be prepared (know what it is going to happen and plan accordingly) and to pay attention. First, to separate two compounds A and B, you must prepare at least three clean receivers, one for the A-enriched fraction, one for the B-enriched fraction, and one for the in-between ‘discard’ fraction. Second, you need to monitor T and the amount of liquid condensing carefully at all times so that you have a good idea when to switch receivers. Finally, don’t be too greedy. Combining materials from a broad T range will give you more distillate, but the distillate will be less enriched. Like so much in life, purity and greed work against each other.

So far we have been describing a distillation procedure that is called simple distillation. The defining feature of a simple distillation is that the liquid boils at one location and all of the resulting gases are immediately condensed and removed. In other words, only one liquid-to-gas transition occurs.

Simple distillation is more of an idealized procedure than a real one, but something approaching a simple distillation can be carried out in the still shown below.

As you saw above, simple distillation of mixtures like cyclohexane-toluene is not highly effective. For example, simple distillation of a 50:50 cyclohexane:toluene mixture initially gives a distillate containing ~80% cyclohexane. This mixture is somewhat enriched in cyclohexane, but it still contains 20% toluene. Worse, the toluene contamination rises as the distillation proceeds.

We could improve on this situation if we could perform a series of simple distillations. For example, distilling a 50:50 Tol:Cy mixture gives (at first) a 20:80 mixture. If we re-distill the 20:80 mixture, this will furnish (at first) a 4:96 mixture. Two sequential distillations gives us much better results than one simple distillation.

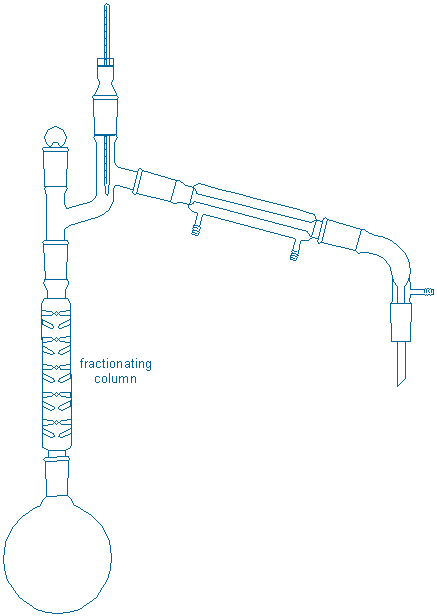
This idea, that sequential distillations are better than simple distillation, provides the motivation for a more difficult distillation procedure called fractional distillation. A typical fractional still is shown below:

The characteristic feature of the fractionating still is the long fractionating column that separates the boiling flask from the thermometer/condenser. The extra surfaces embedded in the fractionating column provide a large hot surface on which gases can condense back into liquids and these ‘enriched’ liquids can re-vaporize upwards without the draining back into the original flask. The effect is roughly equivalent to a sequence of distillations occurring up and down the length of the column, and much better separations are usually achieved.

Unfortunately, fractional distillations are also harder to perform. Longer, high surface area columns provide better separation, but the columns make fractionating stills large and unwieldy. It is also hard to keep fractionating columns sufficiently hot so that distillation occurs everywhere throughout the column and this problem is even more challenging for larger columns (one common problem in a column that fails to get sufficiently hot is “flooding,” the liquid that forms in the column fills the column and prevents the smooth upward passage of gases). Another problem with fractional stills is that they are relative inefficient. It is ALWAYS unsafe to continue a distillation to the point where the boiling flask and fractionating column are dry. Therefore, the distillation must be stopped when there is still a little liquid in the boiling flask. At this point there is still considerable liquid coating the inside of the column (the amount of liquid needed to coat a column’s surfaces completely is referred to as the hold-up volume of the column) and the combined volumes of the boiling flask residue and the hold-up volume represent material that cannot be purified by distillation.

This experiment provides an opportunity to perform and compare the properties of simple and fractional distillations. The idea is partly to collect data that can be used to construct T vs. V graphs for the two procedures like the ones shown above, and also partly to see if you can actually obtain pure samples and reliable boiling point measurements for the two compounds in your unknown mixtures.