Hi, I am Tunc. If you have read this recent post by Jiarong Li, you might remember that we work on signaling pathway reconstruction. This is a better way of saying that we try to determine the many different orders of protein-protein interactions within a cell, from a receptor to a transcription factor, that make up a pathway. In this post, I want to talk about why and how we have combined PathLinker and our work on Directed Acyclic Graphs (DAGs).
PathLinker can find k-many shortest paths from a receptor to a transcription factor. In our graphs, the length of an edge represents the cost of a protein-protein interaction. We assume that evolutionarily, if an interaction is important for the pathway, it will be optimized to happen easily or have a lower cost, meaning that it will be “shorter”. Hence, one could imagine that the chains of interactions or the paths, that are important for the pathways will be shorter, allowing us to frame the reconstruction problem as a shortest-paths problem. PathLinker can find k-many shortest paths very quickly, where k is user-defined, which is nice. However, as k increases, a lot of these paths start to reuse the same edges over and over again, resulting in a decreased amount of information added.
With DAGs, we start with some ground-truth network, find a collection of shortest paths that are not in our network, evaluate them according to some cost function we can customize, pick the path that the cost function thinks is the best, add it to our network and repeat this process many times. This process takes a lot more time than PathLinker and because it has so many parts, changing one thing like the cost function or the ground-truth network can affect the result greatly. This also means that for our program to work properly, we need to be very careful that every part works as we intend it to AND how we intend it to work makes sense biologically.
Even though our long term goal might be to get all of those parts working, one quick idea we could try was to impose some of these criteria to the paths PathLinker quickly generates. To do that, we first ran PathLinker to get 50,000 paths, which seemed like a big enough number of paths, and then we wrote a script to iterate over these paths and choose the ‘acceptable’ ones. Here, the definition of acceptable is customizable, and we have tested it with several definitions to observe how our results change.
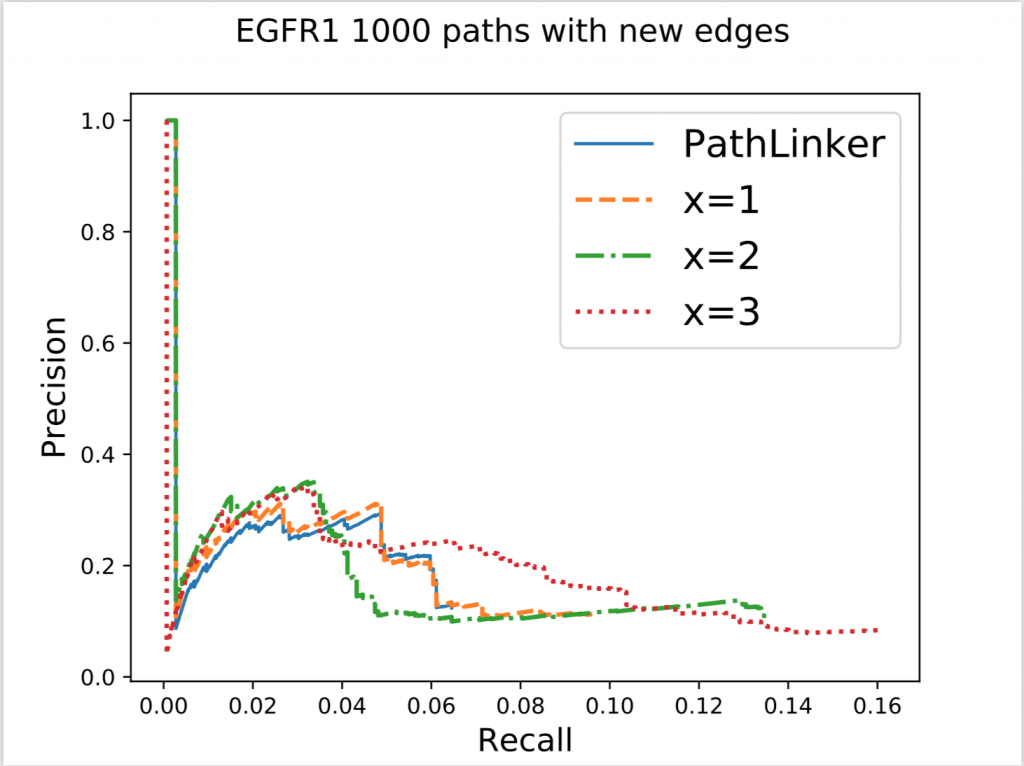
In the figure above, x denotes the minimum number of new edges a path must add for it to be acceptable. Increasing x resulted in an increase of recall without a significant effect on precision. This result wasn’t very surprising because repeated use of false edges does not decrease precision values, each edge is only counted once. Recall increasing also wasn’t very surprising as all we did was to require the addition of new edges, some of which had to be true protein-protein interactions. The real surprising observation we made was when we used this method on different pathways. Epidermal Growth Factor Receptor (EGFR) is a very big pathway, at least in the NetPath database, the other pathways’ data we had were significantly smaller. Consequently, when we used the same method on other pathways, with x = 3 or sometimes even 2, we could never find 1000 acceptable paths. To reiterate, out of 50,000 shortest paths we had originally, there weren’t even 1000 of them that continually added enough new edges to our network. This meant that the reuse of edges in PathLinker was on a very big scale, underlining the potential for our new method.
